El próximo lunes, 14 de noviembre, se producirá la mayor y más brillante Luna desde 1948 y hasta 2034, aunque será muy difícil apreciar la diferencia de tamaño
Ningún planeta del Sistema Solar mantiene una relación relativa tan importante con un satélite como lo hace la Tierra con la Luna. Tal vez los humanos tratamos de devolverle el corazón que perdió cuando se separó violentamente de nuestro mundo. El poder de atracción es enorme, fascinante. Ella, junto con el Sol, ejerce el suyo sobre la Tierra: las mareas. El próximo 14 de noviembre, pondremos de nuevo nuestros ojos en la Luna que, por lo brillante y cercana que estará, llamamos “Superluna”. Un término, por cierto, que se suma, desde hace tan solo unos cinco años, a los cientos de nombres que venimos dando a nuestro exclusivo satélite desde que fuimos capaces de observarlo. La Luna, después de todo, es de la “familia”.
Durante las Superlunas, el diámetro de la Luna llena puede aumentar hasta en un 14%, y su brillo, alrededor de un 30%, respecto a una Luna llena en el apogeo (máxima distancia a la Tierra). La pregunta es ¿podemos percibir el cambio de tamaño a simple vista? La respuesta es que será muy difícil apreciarlo, aunque la Luna será más brillante.
Para responder, debemos calcular el cambio angular aparente (tamaño aparente que tiene la Luna en el cielo si la observamos a simple vista) en la Luna llena. En el mejor de los casos, la diferencia de tamaño en el cielo de la Luna llena en el apogeo y en el perigeo (Superluna) es de 4minutos de arco.
Como referencia, podemos tomar el tamaño que ocupa (en el cielo) nuestro dedo meñique cuando lo observamos con el brazo extendido (ver fig. 2), que es de sesenta minutos de arco (un grado). En promedio, la Luna llena tiene un tamaño angular (tamaño en el cielo) de 30 minutos de arco (¡la mitad del dedo meñique!).

La Luna gira alrededor de la Tierra con un periodo de aproximadamente 28 días, aunque su órbita no es circular -se trata de una elipse-, de ahí que la distancia Luna-Tierra no sea siempre la misma. Además, los parámetros orbitales de la Luna varían con el tiempo, debido principalmente a las influencias gravitatorias del Sol y los planetas. Por esta última razón, siempre que se hable de alguna característica de la órbita lunar deberá referirse a un determinado periodo de tiempo.
Si tomamos el periodo de 5.000 años, desde -1999 hasta 3000, la distancia del perigeo lunar (mínima distancia Tierra-Luna) ha variado entre 356.355 y 370.399 km, mientras que el apogeo lunar (máxima distancia Tierra-Luna), entre 404.042 y 406.725 km (Five Millennium Catalog of Solar Eclipses, Espenak and Meeus, 2009).
Cerca del perigeo
Por definición, se producirá una Superluna si la Luna llena sucede cerca del perigeo lunar (normalmente a menos de dos días). Matemáticamente, podemos definir la distancia relativa de la Luna llena para una órbita determinada (RDfm) como:
RDfm = (Da-Dfm) / (Da-Dp),donde Da es la distancia Luna-Tierra en el apogeo lunar; Dp, la distancia Luna-Tierra en el perigeo lunar; y Dfm,distancia Luna-Tierra en el momento de la Luna llena.
Si la Luna llena ocurre en el momento del perigeo, entonces RDfm es igual a 1, mientras que si la Luna llena transcurre en el apogeo, RDfm es igual a 0. Por definición, tendremos una Superluna si RDfm es igual o mayor que 0,9.
Si bien es cierto que durante las Superlunas la atracción gravitatoria lunar es mayor, el único efecto sobre nuestro planeta lo observaremos en mareas más vivas. El incremento gravitatorio sigue siendo demasiado débil para causar perturbaciones geológicas (terremotos, tsunamis…).
Frecuencia
Si realizamos los cálculos, podemos darnos cuenta de que no es raro que la Luna llena suceda cerca del perigeo. De hecho, suelen ocurrir de 3 a 5 Superlunas en un año (de las 12-13 posibles, ver tabla de astropixels.com). Durante el año 2015 tuvimos cinco Superlunas, mientras que en el año 2016 se producirán 4 (septiembre, octubre, noviembre y diciembre).
El 14 de noviembre de 2016, la Luna llena se producirá a las 13h52m UT (Tiempo Universal). Será la mayor Luna llena en 86 años (1948-2034) y estará situada muy cerca del perigeo (distancia Tierra-Luna llena será de 356.523 km, mientras que en el perigeo lunar será de 356.512km). La mayor Superluna del siglo XXI se producirá el 6 de diciembre del año 2052, con nuestro satélite a una distancia de 356,429 km.
En la situación más favorable, una Superluna tendrá un diámetro de 4 minutos de arco mayor que una Luna llena en el apogeo, es decir, el incremento de diámetro angular de la Superluna es de solo la quinceava parte del tamaño angular de nuestro dedo meñique. Realmente muy difícil distinguirlo a simple vista (ver figura 2).
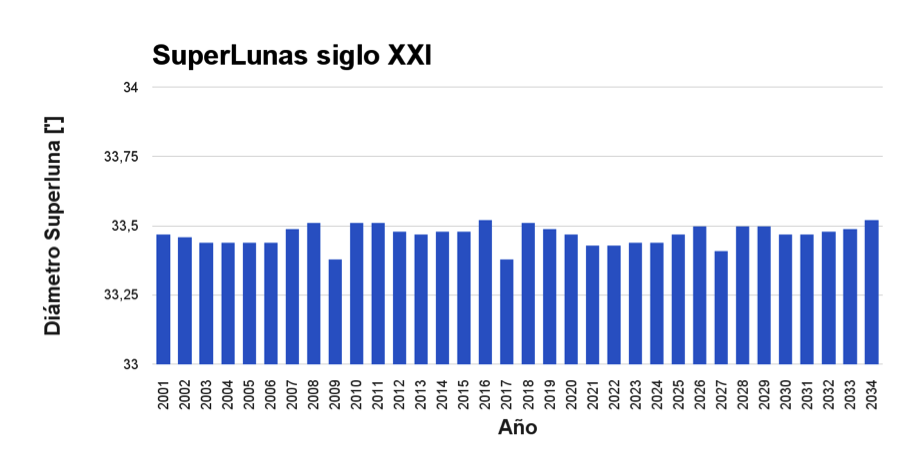
También podemos comparar la variación de tamaños de las mayores Superlunas anuales entre los años 2001 y 2038 (ver figuras 2 y 3). La diferencia máxima se produce entre la Superluna del año 2017 y la de 2016 y es de tan solo 8 segundos de arco. Es imposible percibir esta variación a simple vista, como se muestra en la figura 1.
Material audiovisual
-Imágenes Superlunas
https://flic.kr/s/aHsk13TxjS
-Sombra Teide y SuperLuna
https://youtu.be/4RxBICUyvHc?list=PL6oc5e7lSjeLcIvr_0sbFuDTB xuMqZJgN
Autores:
Miquel Serra-Ricart es astrónomo del Instituto de Astrofísica de Canarias (IAC), doctor en Ciencias Físicas y Administrador del Observatorio del Teide. Forma parte del Grupo de investigación del Sistema Solar del IAC dirigido por Javier Licandro.
Isabel Paz Menéndez es periodista. En la actualidad se encarga de la comunicación del canal del cielo sky-live.tv.
Este artículo ha sido publicado en la versión digital del periódico El País/Materia con fecha 13 de noviembre de 2016:
http://elpais.com/elpais/2016/11/13/ciencia/1479033772_910377.html

